
2025.07.17 / 넥스트플랫폼 동준상 프로
- QGSS25 D10: (작성 예정)
- QGSS25 D9: IBM qLDPC 코드 기반의 오류 내성 양자 컴퓨팅
- QGSS25 D8: 양자 오류 정정, 쇼어 코드 기반의 오류 정정, 안정기
- QGSS25 D7: 양자 컴퓨팅 정확도 개선, 샘플링 기반 양자 대각화
- QGSS25 D6: 양자 벤치마킹, 오류 감지 +
- QGSS25 D5: 실용적 양자 알고리즘과 연산 기법
QGSS25 D9: IBM qLDPC 코드 기반의 오류 내성 양자 컴퓨팅
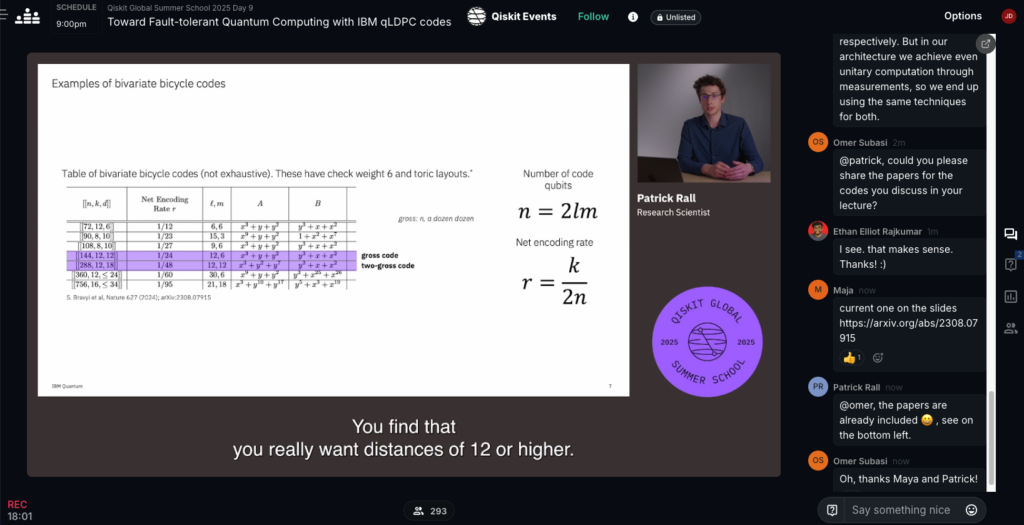
S1. Toward Fault-tolerant Quantum Computing with IBM qLDPC codes
- Patrick Rall, Research Scientist
1. 왜 양자 컴퓨터는 오류에 취약한가?
- 양자 비트(Qubit)는 노이즈(잡음)에 민감함 → 열, 자기장, 측정 등 작은 외부 요인에도 영향을 받음
- 양자 연산은 정확한 제어와 정밀한 타이밍이 요구됨
- 에러 누적 → 연산 실패 → 100개 연산 중 1개만 틀려도 전체 계산 결과가 무의미해질 수 있음

2. 기존 컴퓨터와 양자 컴퓨트의 안정성, 오류 비교
| 구분 | 기존의 컴퓨터 | 양자 컴퓨터 |
|---|---|---|
| 비트 안정성 | 매우 높음 | 매우 낮음 |
| 오류 허용 수준 | 낮음 (에러 적음) | 높음 (에러 많음) |
| 오류 교정 방식 | 간단한 리트라이 | 정교한 코딩 및 보정 필요 |
3. 오류를 감지하고 고치는 법: FTQC의 핵심 원리
- 양자 오류 수정(QEC, Quantum Error Correction)
- → 하나의 논리 큐비트(logical qubit)를 여러 개의 물리 큐비트로 표현
- → 에러를 감지하고 자동으로 보정
- 결함 허용(Fault Tolerance)
- → 오류가 일부 발생하더라도 전체 계산이 정확하게 유지되도록 설계
- → 개별 연산, 측정, 큐비트 이동 등 모든 연산 단계에서 오류 허용
- 주요 기법 예시:
- Shor Code (9-Qubit)
- Surface Code (격자 구조) → 실용화 가능성이 높음
- Stabilizer Formalism → 오류를 감지하는 수학적 도구 사용

4. FTQC를 향한 도전과 미래
- Fault-tolerant Quantum Computing, 어디까지 왔나?
- 현재 대부분의 양자 하드웨어는 Noisy Intermediate-Scale Quantum (NISQ) → 아직 완전한 FTQC는 어려움
- FTQC 구현을 위해 필요한 요소
- 1. 수천 ~ 수백만 개의 고품질 물리 큐비트
- 2. 빠르고 정밀한 오류 수정 알고리즘
- 3. 에러율 낮은 양자 게이트
- 미래 전망:
- IBM, Google, IonQ 등 → Surface Code 기반 FTQC 실현 목표
- Fault tolerance는 대규모 유용한 양자 알고리즘의 전제조건
- FTQC는 양자 우월성(Quantum Supremacy)을 실용화로 연결하는 다리
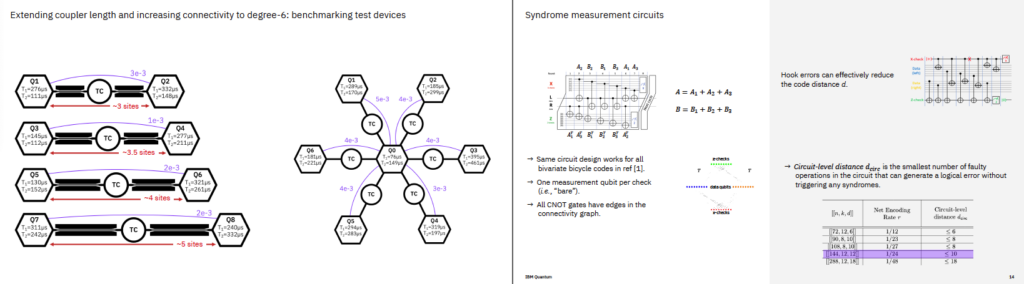
QGSS25 D8: 양자 오류 정정, 쇼어 코드 기반의 오류 정정, 안정기 및 CSS 코드 활용
S1. The History of Quantum Error Correction
- Barbara Terhal
1. 양자 오류 보정이 필요한 이유
- 양자 컴퓨터는 매우 민감
- Qubit은 외부 환경과 쉽게 얽힘 (entanglement) → 정보 손실
- 일반 오류: 비트 플립 (|0⟩ ↔ |1⟩), 위상 플립 (|+⟩ ↔ |−⟩), 혼합 잡음 (decoherence)
- 복사 불가: 양자 상태는 고전 정보처럼 복사할 수 없음 (no-cloning theorem)
- 그래서 양자 정보를 보호하는 방법으로 QEC 필요
2. 양자 오류 보정의 핵심 아이디어
- 중복 저장 → 오류 검출 & 보정
- 단일 qubit을 여러 qubit에 인코딩하여 오류를 감지 가능하게 만듦
- 예시: 3중 비트 플립 코드 |0⟩ → |000⟩, |1⟩ → |111⟩
- 오류 발생시: 예) |010⟩ → 다수결로 복원
- Syndrome 측정: 오류는 직접 측정하지 않고, qubit 간 관계(패리티)를 측정해 오류 여부 확인 >> 측정은 상태를 망가뜨리지 않음
- 오류 감지 후 → 보정 게이트를 적용해 원래 상태로 복원
3. 대표적인 QEC 코드와 미래 전망
- Shor Code: 9 qubit 기반, 비트+위상 플립 모두 보정 가능
- Steane Code: 7 qubit 기반, 실용성과 구조적 간결성 우수
- Surface Code: 2D 격자 구조, 실제 하드웨어 구현에 적합
- QEC의 목표: 오류율 ↓ → 더 깊은 회로 실행 가능
- FTQC (Fault-Tolerant Quantum Computing) 실현의 핵심 기술
- 향후 과제: 물리적 qubit 수를 줄이면서 보정 효율을 높이는 low-overhead QEC 발전, 실시간 오류 추적 및 자동 보정 기술 개발
S2. Basics of Quantum Error Correction Part I: Correcting Errors with the Shor code
- John Watrous



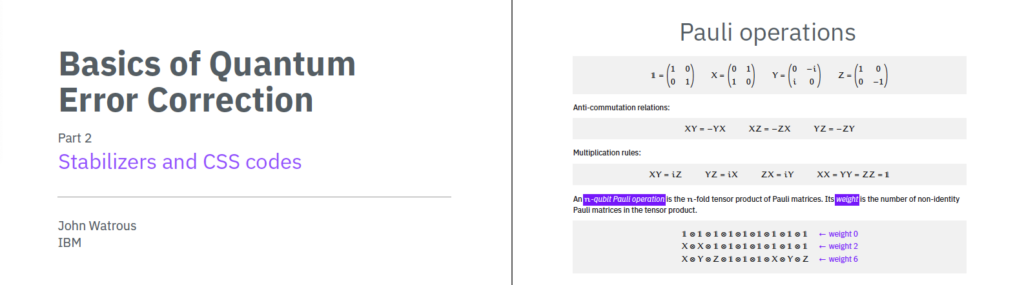
S3. Basics of Quantum Error Correction II: Stabilizers and CSS codes
- John Watrous


QGSS25 D7: 양자 컴퓨팅 정확도 개선, 샘플링 기반 양자 대각화 방법
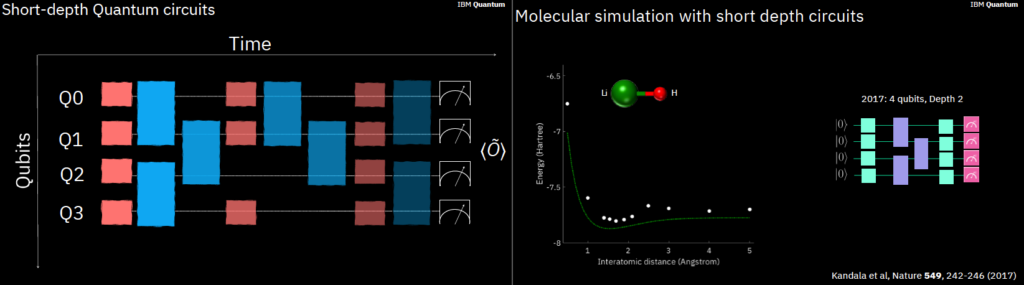
S1. Accurate Quantum Computing in the Utility Era
- Abhinav Kandala


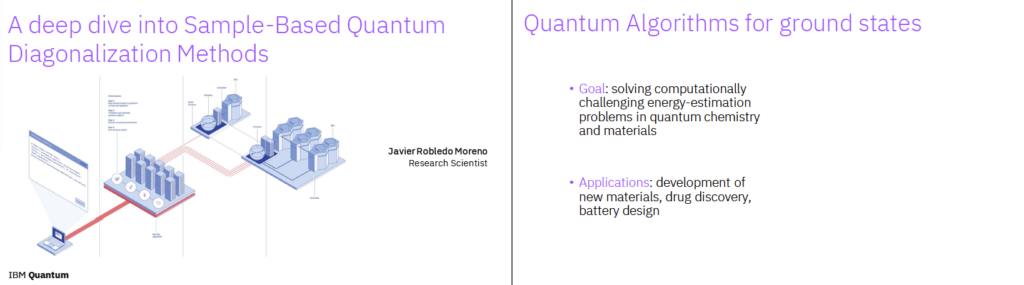
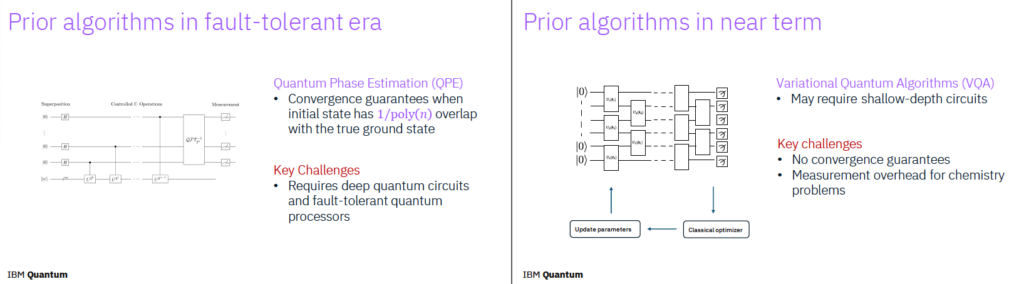
S2. A deep dive into Sample-Based Quantum Diagonalization Methods
- Javier Robledo Moreno
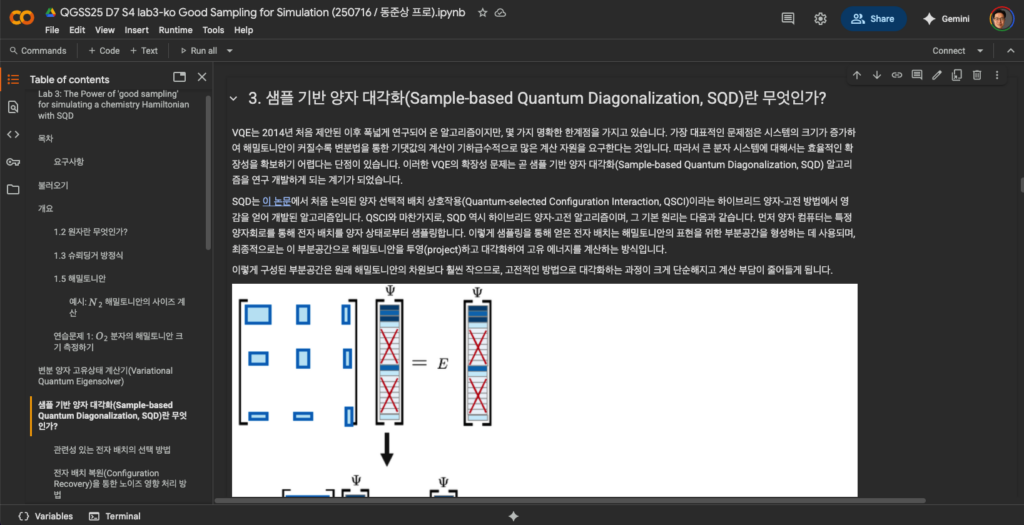
- 샘플 기반 양자 대각화 기법: 양자 회로나 양자 측정을 통해 시스템의 행렬을 샘플링하여 고유값을 추정하고, 이를 통해 시스템을 분석하는 기법
- Sample-Based (샘플 기반): 전통적인 계산 대신, 양자 측정이나 확률적 샘플링을 이용해 정보를 얻는 접근 방식
- Quantum Diagonalization (양자 대각화): 양자 시스템의 해밀토니안(Hamiltonian)이나 행렬을 고유값 분해(대각화)하여, 에너지 준위나 동역학을 분석하는 방법

S3. Good Sampling for Simulation
- QGSS25 D7 S4 lab3-ko Good Sampling for Simulation (250716 / 동준상 프로).ipynb
- https://colab.research.google.com/drive/14D4ONbc7enkn-rNZH33jwjCGMIsaAqq-?usp=sharing
QGSS25 D6: 양자 벤치마킹, 오류 감지 +
S1. Quantum Benchmarking
- Andre He & Majo Lozano
1. 양자 벤치마킹 개요
- 강사: Andre He (IBM Quantum 하드웨어 엔지니어)
- 목표: 양자 컴퓨터의 잡음(noise) 특성을 이해하고, 정량화된 방식으로 성능 측정하는 방법 습득
- 주요 주제
- Qubit, Quantum Gate, Noise 이해
- 시스템/서브시스템 수준 벤치마킹
- T1, T2, Readout 오류, Tomography, Randomized Benchmarking 등
2. Qubit과 Quantum Gate
- Qubit: 양자 정보의 기본 단위, 상태는 |0⟩과 |1⟩의 중첩으로 표현
- 상태 표현: Bloch Sphere상 벡터로 시각화
- Quantum Gate: 상태벡터를 회전시키는 유니터리 연산
- 이상적인 게이트: 벡터 길이 유지하며 정확하게 회전
- 실제 게이트: 잡음으로 인해 회전 불완전 → 오류 발생
3. 양자 잡음이란?
- 양자 연산: CPTP(Completely Positive, Trace Preserving) Map으로 기술
- 잡음의 영향
- 과도 회전, 불완전 회전 (over/under-rotation)
- 벡터 크기 축소 → 상태 혼돈 증가
- 잡음은 피할 수 없으므로 정확히 측정하고 보정해야 함
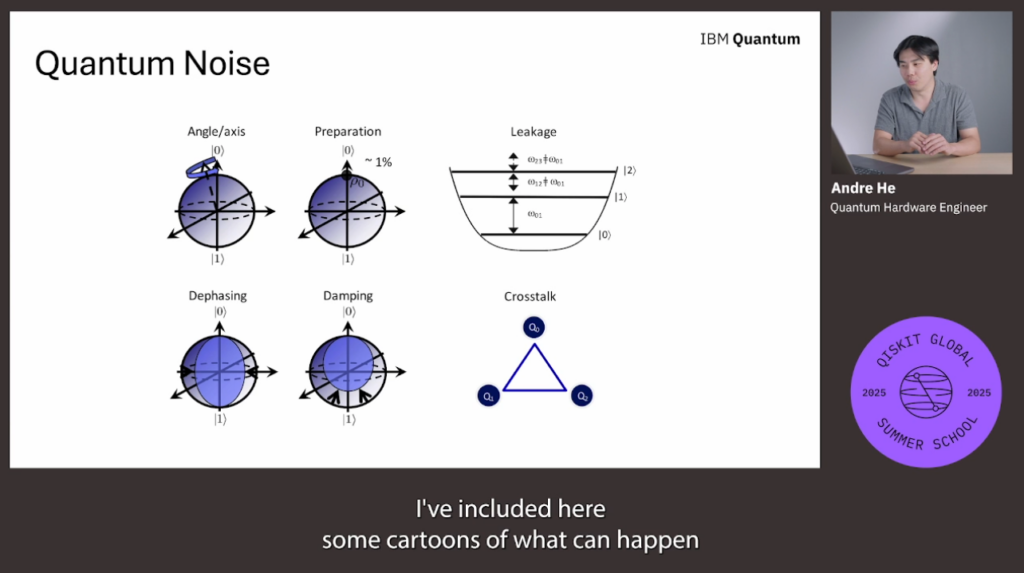
4. 다양한 잡음 유형
- 비트/위상/복합 플립 (Pauli X, Y, Z): 축 반사로 상태 변경
- Depolarizing Noise: 상태를 섞어 중심으로 수축
- Amplitude Damping: 에너지 손실로 |1⟩ → |0⟩
- Phase Damping: 위상 정보 손실로 XY평면 축소
5. 양자 잡음 요약
| 잡음 종류 | 설명 |
|---|---|
| T1 (Relaxation) | 에너지 방출, |
| T2 (Dephasing) | 위상 손실, coherence 붕괴 |
| 게이트 보정 오류 | 과도/부족 회전 |
| SPAM 오류 | 잘못된 초기화/측정 |
| 크로스토크 | 주변 qubit 간 간섭 |
| 리키지/비마르코프 잡음 | 시스템 밖으로 빠짐, 과거 이력의존 오류 |
6. 왜 노이즈 특성 분석이 중요한가?
- 성능 제한 요인: 잡음이 계산 결과를 왜곡
- 정확한 모델링 필요성
- 오류 완화(error mitigation)
- 현실적 시뮬레이션
- 회로 배치 최적화
7. 장치 수준 벤치마크: T1 & T2
T1 (Relaxation Time)
- |1⟩ 준비 → 대기시간 후 측정
- 시간에 따른 P1(t) 분석 → 지수함수로 피팅
T2 (Dephasing Time)
- 𝜋/2 gate → echo sequence → 측정
- P0(t) 분석으로 위상 coherence 지속시간 측정
8. 측정 오류와 보정
- Readout Error: 상태를 잘못 읽는 확률
- 보정 방법
- 오류 행렬 M 계산 → M⁻¹ 이용해 참 확률 복원
- Quasiprobability Inversion: 측정결과에 확률 가중치 부여
- 주로 1~2 qubit 단위로 독립 보정 → 확장성 확보
9. 서브시스템 수준: 상태/과정 토모그래피
Quantum State Tomography
- 상태를 다양한 기준축(X, Y, Z)에서 다수 측정
- 밀도 행렬(density matrix) 복원
Quantum Process Tomography
- 입력상태 → 연산 수행 → 출력 상태 복원
- 전체 연산(게이트)의 행동 분석
주의: 큐비트 수 늘면 측정 조합이 지수적 증가 → 리소스 소모 큼
10. Randomized Benchmarking
- 목적: 평균적인 게이트 오류율 평가
- 방법
- 랜덤 Clifford gate 시퀀스 생성
- 마지막에 역게이트 삽입 → |0⟩ 복원 기대
- 반복 측정 → 평균 오류 추정
- 2Q RB: 2큐비트 Clifford 그룹 적용 → 1Q+2Q 오류 조합 추정
S2. Low-overhead Error Detection with Spacetime Codes
- Ali Javadi / Principal Research Scientist IBM Quantum
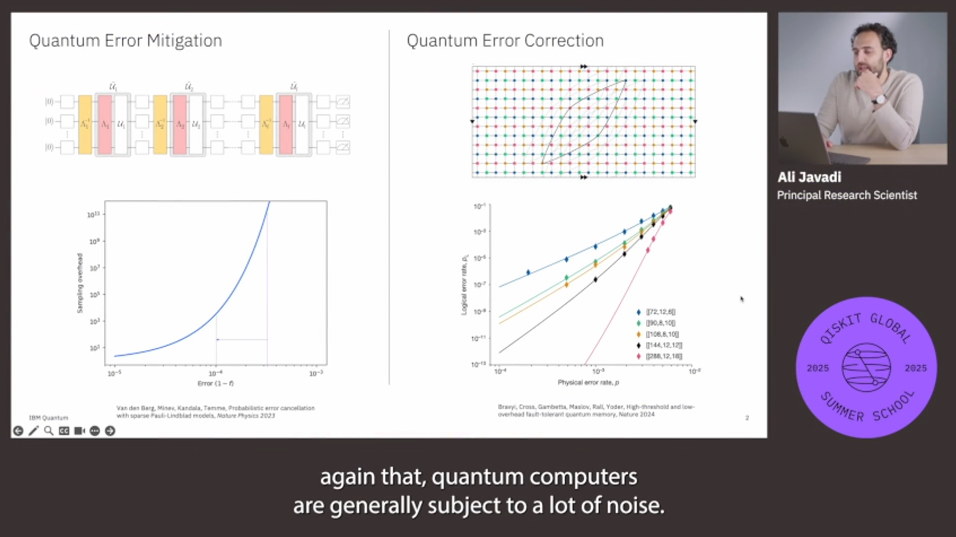
1. 개요: Spacetime Code란?
- 오류 검출을 위한 새로운 접근법
- 오류 검출은 샘플 수 감소를 위해 여분의 큐비트 사용
- 단일 샷(single-shot) 방식이지만, 회로가 비효율적이면 오류를 더 증가시킬 수 있음
- 해결책: 효율적이면서도 오류 검출 효과가 높은 spacetime 기반 체크 회로
2. Pauli 체크 기반 오류 검출 복습
- Coherent Pauli Check 방식:
- 여분의 큐비트와 Clifford 회로 얽힘
- 측정을 통해 Pauli 연산이 올바르게 작용했는지 판별
- 문제점: 체크 수 증가 → 오버헤드 증가, 검출율 저하
- Spacetime 코드 도입 이유: 효율적이고 선택적인 검출 가능
3. Spacetime Checks vs 기존 체크 방식
- One-sided Check (기존): 회로의 오른쪽에만 오류 검출
- Spacetime Check: 시간 + 공간에 걸쳐 Pauli 체크를 분산
- 예: 특정 지점의 오류만 검출하는 게 아니라, 동선 전체에서 오류 감지 가능
4. Spacetime Check 동작 방식
- Payload 준비
- 인접한 체크 큐비트와 연결 가능한 선 선택
- 해당 선에서 유효한 저무게 Pauli 연산 찾기
- 체크 실행
- 체크의 누적 효과(“cumulant”) 계산 → 범위 평가
- 스코어링 → 반복
- 검출 범위 시각화: 오류 발생 위치의 ⅔ 이상을 탐지 가능
5. 시각화: Spacetime Checks & Cumulants
- 개념: Clifford 회로에 시간-공간을 따라 Pauli 연산을 “흩뿌리는(sprinkle)” 방식
- 핵심: 저무게(low-weight) 체크를 찾는 디코딩 문제 해결로 하드웨어 효율성 확보
- 요약: 체크를 공간적으로 분산시키고 시간적으로 싸게 배치
6. 적용 대상 및 효과
- 적용 대상: Clifford 및 Clifford 기반 회로
- 대표 사례: Magic-state 기반 회로, Clifford 회로 샘플링, 그래프 상태 생성, 측정 기반 양자 계산(MBQC) 등
- 기존보다 샘플과 회로 오버헤드 적음 + 검출 효과 큼
7. Beyond Clifford: 비-Clifford 회로에도 적용 가능?
- 비-Clifford 연산(Rₚ) 등장 시:
- 체크는 해당 연산과 교환 가능(commute) 해야 유효
- 제약조건 증가 → 유효 체크 공간 지수적 감소
- 제한적이지만 여전히 사용 가능
8. 응용: GHZ 상태 준비 최적화
- GHZ 상태: 시스템 품질 벤치마크에 자주 사용됨
- 특징: 순열 불변 + 간단한 ZZ 체크 구조
최적화 알고리즘
- 오류 높은 노드/엣지 제거
- 각 큐비트에서 BFS 트리 생성 → 최단 깊이 GHZ 선택
- 일부 노드 무작위 차단 → 다시 BFS
- 유효 체크 생성 및 범위 계산
- 반복 → 최적 커버리지 탐색
9. GHZ 상태의 Fidelity 검증
- 기존 방법: 직접 Fidelity 추정
- 새 접근: 회전 각도 변화에 따른 진동(Oscillation) 분석
- 연구 진행 중 (Seif, Wei, Martiel 등) → 두 방법 간 연계 가능성 높음
10. 결론 및 향후 과제
- Spacetime 기반 Pauli 체크로 효율적인 오류 검출 가능
- 모든 큐비트 연결 그래프에 적용 가능
- 실험 결과와 시뮬레이션이 잘 일치
- GHZ 100+ 큐비트 및 2.5k 게이트 그래프 상태 실험 실현
열린 질문
- 체크를 오류 보정까지 확장할 수 있을까?
- 회로 구조의 규칙성 이용해 더 나은 체크 설계 가능할까?
S3. Live Q&A Session
- Andre He, Majo Lozano, & Ali Javadi
QGSS25 D5: 실용적 양자 알고리즘과 연산 기법
S1: Practical Quantum Algorithms: VQA, VQE, QAOA
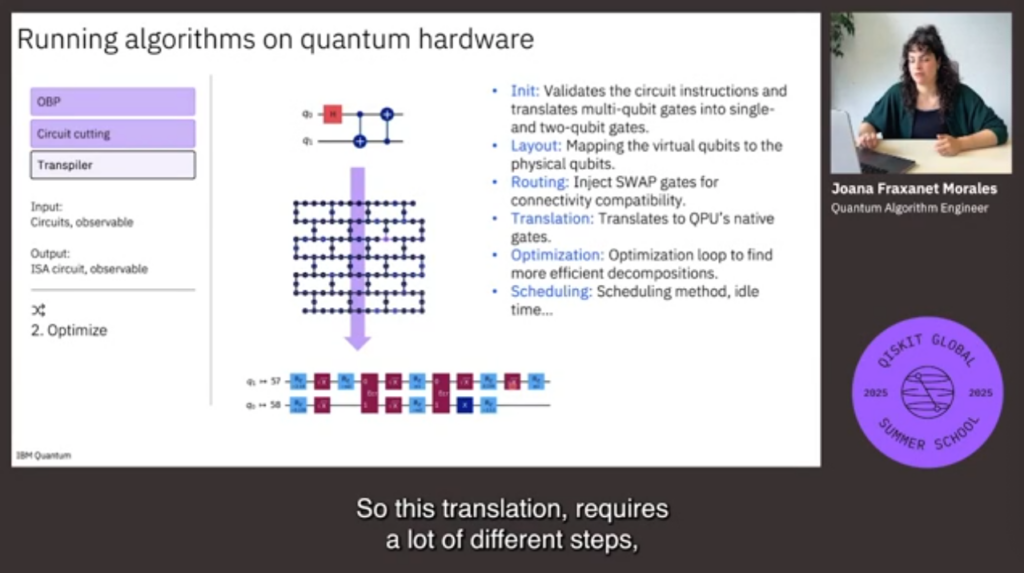
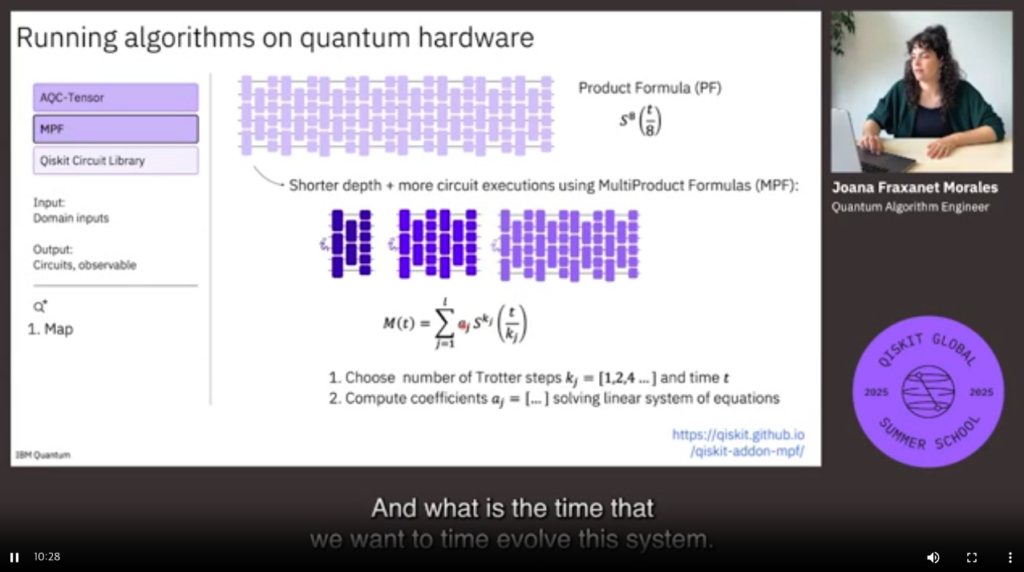

1. Variational Quantum Algorithms (VQA)
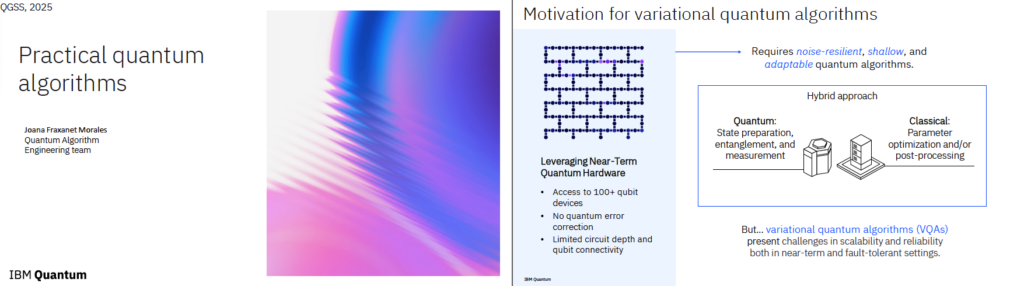
VQA는 현재의 제한된 양자 하드웨어에서도 실질적으로 사용할 수 있는 하이브리드 알고리즘입니다. 일부 연산은 양자 컴퓨터가, 일부 연산은 고전 컴퓨터가 수행하며 서로 보완합니다.
- 왜 필요한가?
- 현재 양자 컴퓨터는 오류가 많고 큐비트 수가 적기 때문에, 완전한 양자 알고리즘은 실행이 어렵습니다.
- VQA는 잡음에 강하고, **얕은 회로(depth가 작음)**를 사용하며, 다양한 문제에 유연하게 적용 가능합니다.
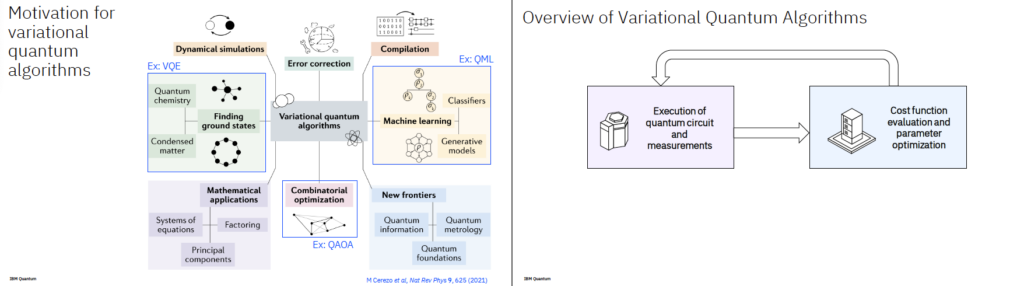
- 적용 분야
- 양자 오류 정정
- 조합 최적화 문제 (예: 물류, 네트워크 최적화 등)
- 양자 화학 시뮬레이션
- 양자 회로 컴파일
- 양자 머신러닝
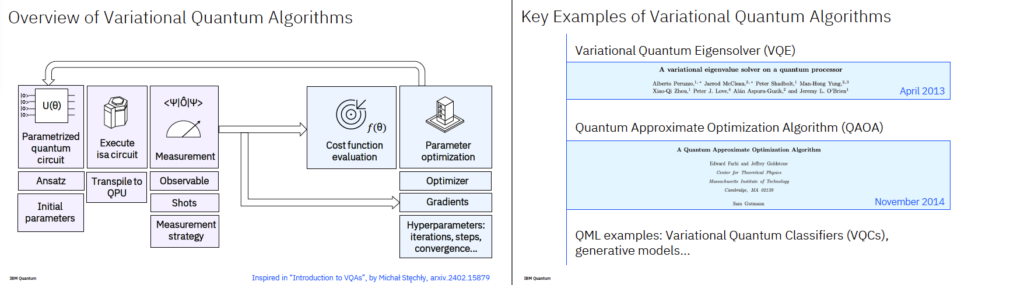
- 핵심 구조
- Parameterized Quantum Circuit (Ansatz):
파라미터를 가진 양자 회로를 구성하여 상태를 생성 - 측정 (Measurement):
양자 상태를 측정하여 결과값을 수집 - 비용 함수 계산 (Cost Function):
측정값으로부터 성능(비용)을 계산 - 최적화 (Optimization):
고전 컴퓨터가 비용을 줄이도록 파라미터를 조정 - 반복 실행:
위 과정을 여러 번 반복하여 최적의 파라미터를 찾음
- Parameterized Quantum Circuit (Ansatz):
2. VQE: Variational Quantum Eigensolver
특정 양자 시스템의 **기저 에너지(Ground State Energy)**를 찾는 데 사용되는 알고리즘. 양자화학, 재료 과학, 약물 설계에 유용합니다.
- 왜 중요한가?
- 분자의 안정성이나 반응성 등을 예측하려면 기저 상태 에너지 계산이 필요
- 전통적인 컴퓨터로는 매우 복잡한 분자 시스템의 에너지를 정확히 계산하기 어려움
- VQE는 양자 상태로부터 기저 에너지를 효과적으로 추정 가능
- Qiskit에서 VQE 구현 가능
- 다양한 Ansatz, 옵티마이저, 시뮬레이터 선택 가능
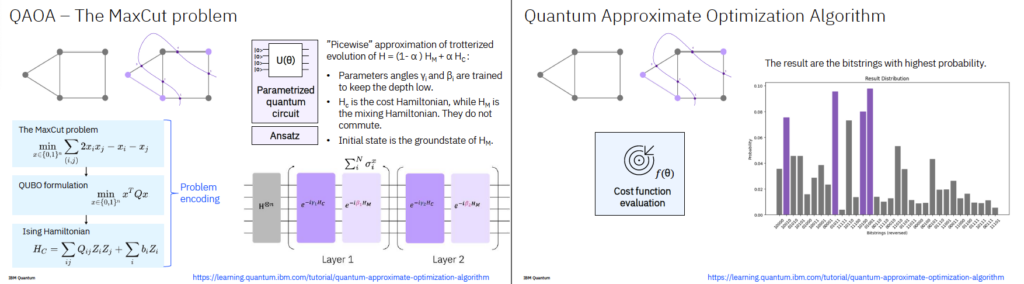
3. QAOA: Quantum Approximate Optimization Algorithm
그래프 이론 등의 조합 최적화 문제를 해결하기 위한 양자 알고리즘. MaxCut 문제가 대표 예시입니다.
- MaxCut 문제란?
- 그래프의 노드들을 두 그룹으로 나눠서, 연결된 간선이 최대한 많이 두 그룹 사이에 놓이도록 분할
- 현실 세계에서는 네트워크 설계, 일정 배정, 전력망 구성 등 다양한 분야에 적용
- QAOA 특징
- 양자 회로로 문제를 모델링하고, 최적화된 해를 근사적으로 구함
- 향후 양자 우위(quantum advantage) 실현 가능성이 높은 분야 중 하나
- **AQC (Adiabatic Quantum Computing)**과 연계
- QAOA는 AQC에서 아이디어를 차용했으며, 디지털 방식으로 구현
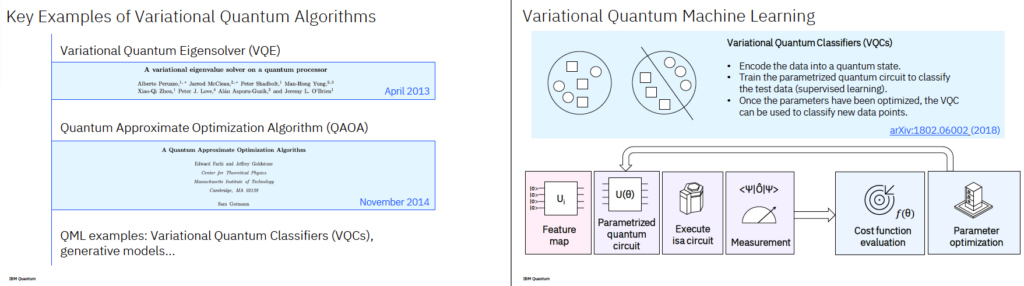
4. Variational Quantum Machine Learning
입문 설명: 양자 회로를 머신러닝 모델처럼 파라미터화하고, 고전적인 방법으로 학습을 수행
- 예: 양자 신경망, 양자 분류기 등
- 양자 회로가 데이터를 임베딩하고, 고전 알고리즘이 파라미터를 업데이트
5. Qiskit 실습
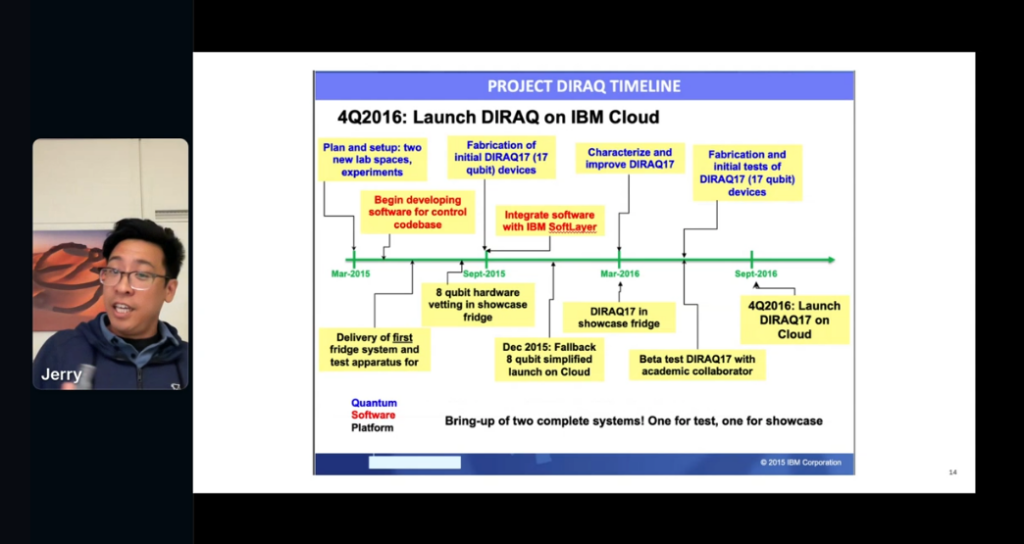
S4: Quantum Computers on the Cloud by Jerry Chow
지속적으로 업데이트되는 포스트입니다. / 첫 포스팅: 250710 / 이 포스트에 대한 문의: naebon@naver.com



