- QGSS25 D6: 양자 벤치마킹, 오류 감지 +
- QGSS25 D5: 실용적 양자 알고리즘과 연산 기법
QGSS25 D6: 양자 벤치마킹, 오류 감지 +
S1. Quantum Benchmarking
- Andre He & Majo Lozano
1. 양자 벤치마킹 개요
- 강사: Andre He (IBM Quantum 하드웨어 엔지니어)
- 목표: 양자 컴퓨터의 잡음(noise) 특성을 이해하고, 정량화된 방식으로 성능 측정하는 방법 습득
- 주요 주제
- Qubit, Quantum Gate, Noise 이해
- 시스템/서브시스템 수준 벤치마킹
- T1, T2, Readout 오류, Tomography, Randomized Benchmarking 등
2. Qubit과 Quantum Gate
- Qubit: 양자 정보의 기본 단위, 상태는 |0⟩과 |1⟩의 중첩으로 표현
- 상태 표현: Bloch Sphere상 벡터로 시각화
- Quantum Gate: 상태벡터를 회전시키는 유니터리 연산
- 이상적인 게이트: 벡터 길이 유지하며 정확하게 회전
- 실제 게이트: 잡음으로 인해 회전 불완전 → 오류 발생
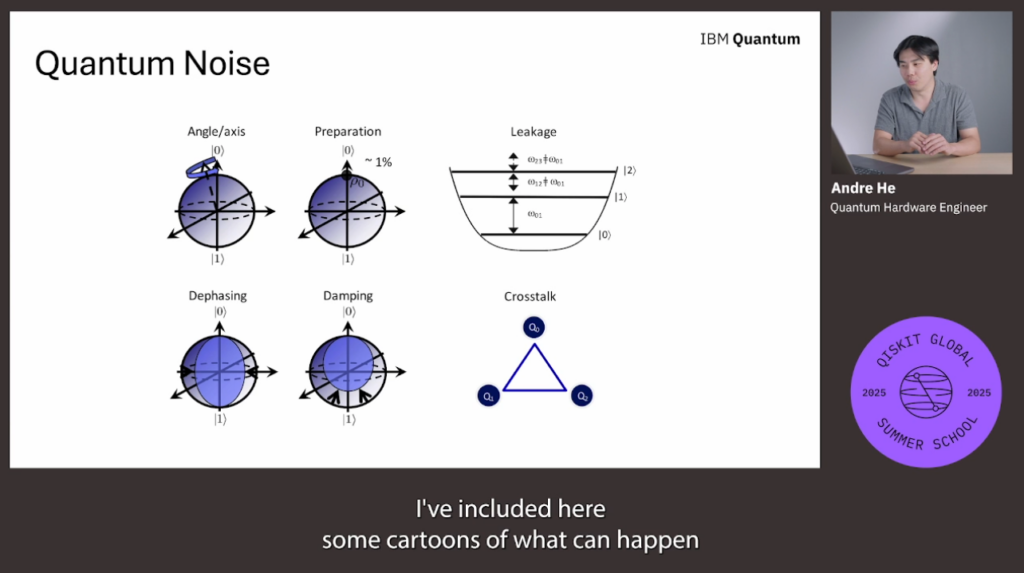
3. 양자 잡음이란?
- 양자 연산: CPTP(Completely Positive, Trace Preserving) Map으로 기술
- 잡음의 영향
- 과도 회전, 불완전 회전 (over/under-rotation)
- 벡터 크기 축소 → 상태 혼돈 증가
- 잡음은 피할 수 없으므로 정확히 측정하고 보정해야 함
4. 다양한 잡음 유형
- 비트/위상/복합 플립 (Pauli X, Y, Z): 축 반사로 상태 변경
- Depolarizing Noise: 상태를 섞어 중심으로 수축
- Amplitude Damping: 에너지 손실로 |1⟩ → |0⟩
- Phase Damping: 위상 정보 손실로 XY평면 축소
5. 양자 잡음 요약
| 잡음 종류 | 설명 |
|---|---|
| T1 (Relaxation) | 에너지 방출, |
| T2 (Dephasing) | 위상 손실, coherence 붕괴 |
| 게이트 보정 오류 | 과도/부족 회전 |
| SPAM 오류 | 잘못된 초기화/측정 |
| 크로스토크 | 주변 qubit 간 간섭 |
| 리키지/비마르코프 잡음 | 시스템 밖으로 빠짐, 과거 이력의존 오류 |
6. 왜 노이즈 특성 분석이 중요한가?
- 성능 제한 요인: 잡음이 계산 결과를 왜곡
- 정확한 모델링 필요성
- 오류 완화(error mitigation)
- 현실적 시뮬레이션
- 회로 배치 최적화
7. 장치 수준 벤치마크: T1 & T2
T1 (Relaxation Time)
- |1⟩ 준비 → 대기시간 후 측정
- 시간에 따른 P1(t) 분석 → 지수함수로 피팅
T2 (Dephasing Time)
- 𝜋/2 gate → echo sequence → 측정
- P0(t) 분석으로 위상 coherence 지속시간 측정
8. 측정 오류와 보정
- Readout Error: 상태를 잘못 읽는 확률
- 보정 방법
- 오류 행렬 M 계산 → M⁻¹ 이용해 참 확률 복원
- Quasiprobability Inversion: 측정결과에 확률 가중치 부여
- 주로 1~2 qubit 단위로 독립 보정 → 확장성 확보
9. 서브시스템 수준: 상태/과정 토모그래피
Quantum State Tomography
- 상태를 다양한 기준축(X, Y, Z)에서 다수 측정
- 밀도 행렬(density matrix) 복원
Quantum Process Tomography
- 입력상태 → 연산 수행 → 출력 상태 복원
- 전체 연산(게이트)의 행동 분석
주의: 큐비트 수 늘면 측정 조합이 지수적 증가 → 리소스 소모 큼
10. Randomized Benchmarking
- 목적: 평균적인 게이트 오류율 평가
- 방법
- 랜덤 Clifford gate 시퀀스 생성
- 마지막에 역게이트 삽입 → |0⟩ 복원 기대
- 반복 측정 → 평균 오류 추정
- 2Q RB: 2큐비트 Clifford 그룹 적용 → 1Q+2Q 오류 조합 추정
S2. Low-overhead Error Detection with Spacetime Codes
- Ali Javadi
S3. Live Q&A Session
- Andre He, Majo Lozano, & Ali Javadi
QGSS25 D5: 실용적 양자 알고리즘과 연산 기법
S1: Practical Quantum Algorithms: VQA, VQE, QAOA
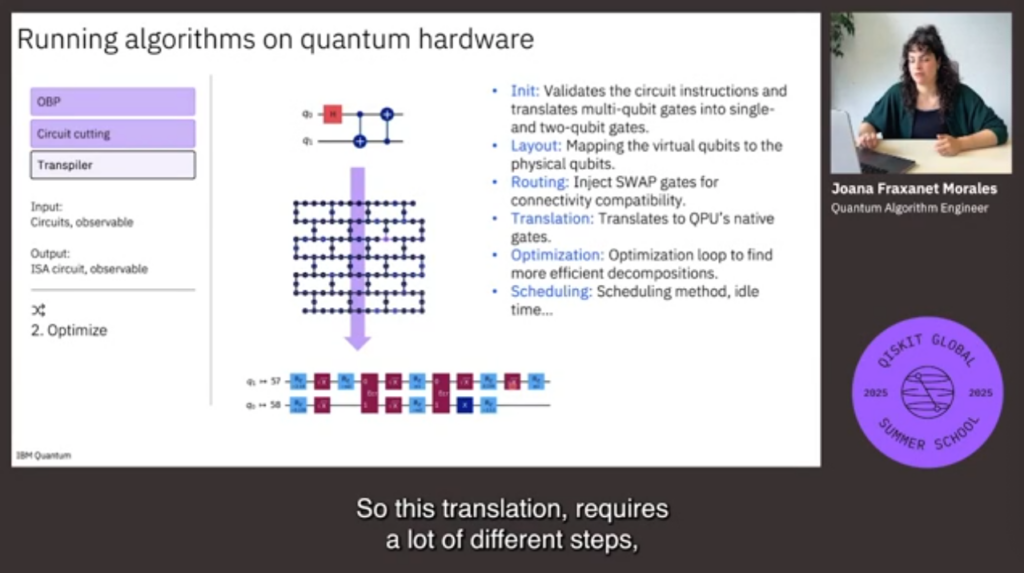
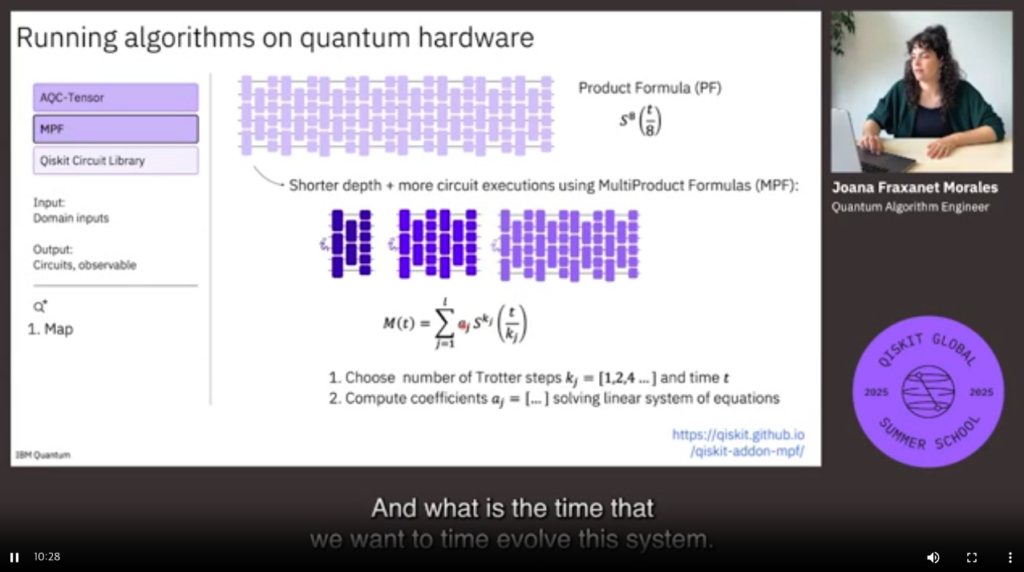
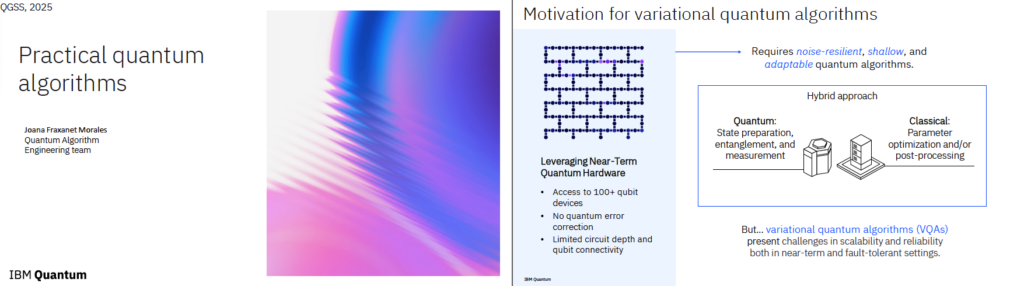
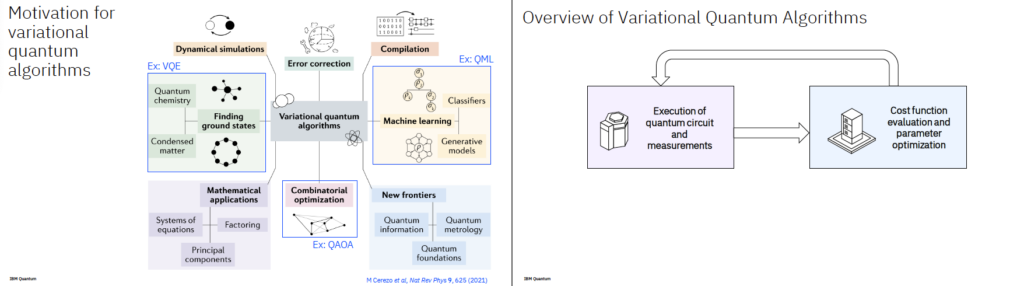
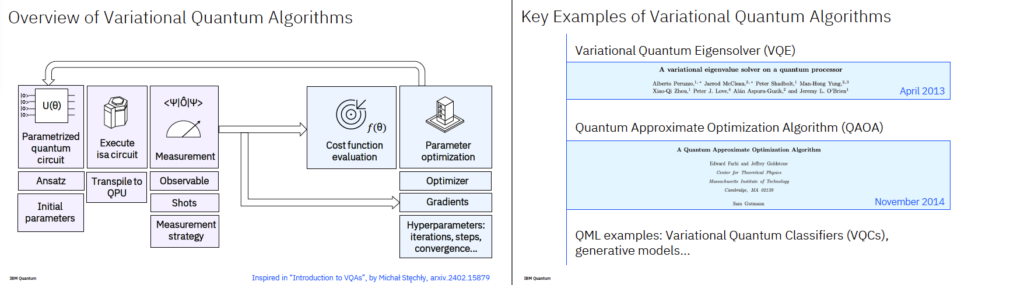

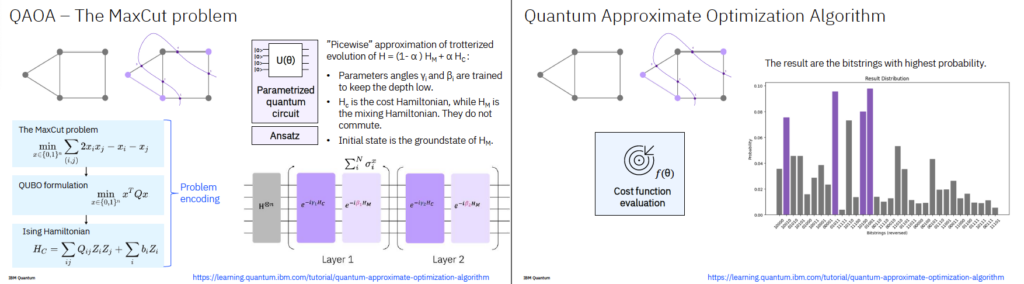
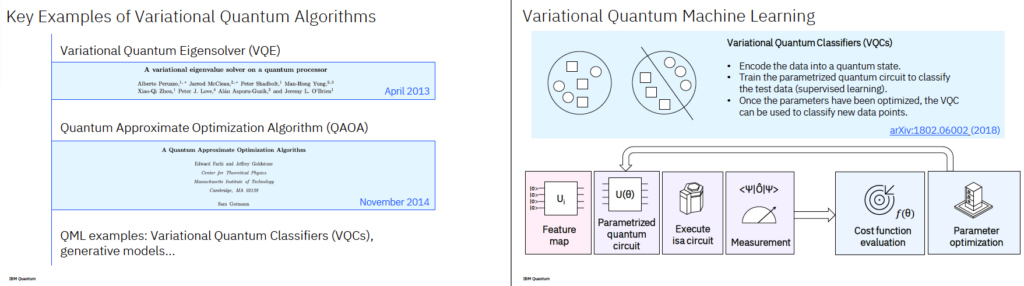
1. Variational Quantum Algorithms (VQA)
VQA는 현재의 제한된 양자 하드웨어에서도 실질적으로 사용할 수 있는 하이브리드 알고리즘입니다. 일부 연산은 양자 컴퓨터가, 일부 연산은 고전 컴퓨터가 수행하며 서로 보완합니다.
- 왜 필요한가?
- 현재 양자 컴퓨터는 오류가 많고 큐비트 수가 적기 때문에, 완전한 양자 알고리즘은 실행이 어렵습니다.
- VQA는 잡음에 강하고, **얕은 회로(depth가 작음)**를 사용하며, 다양한 문제에 유연하게 적용 가능합니다.
- 적용 분야
- 양자 오류 정정
- 조합 최적화 문제 (예: 물류, 네트워크 최적화 등)
- 양자 화학 시뮬레이션
- 양자 회로 컴파일
- 양자 머신러닝
- 핵심 구조
- Parameterized Quantum Circuit (Ansatz):
파라미터를 가진 양자 회로를 구성하여 상태를 생성 - 측정 (Measurement):
양자 상태를 측정하여 결과값을 수집 - 비용 함수 계산 (Cost Function):
측정값으로부터 성능(비용)을 계산 - 최적화 (Optimization):
고전 컴퓨터가 비용을 줄이도록 파라미터를 조정 - 반복 실행:
위 과정을 여러 번 반복하여 최적의 파라미터를 찾음
- Parameterized Quantum Circuit (Ansatz):
2. VQE: Variational Quantum Eigensolver
특정 양자 시스템의 **기저 에너지(Ground State Energy)**를 찾는 데 사용되는 알고리즘. 양자화학, 재료 과학, 약물 설계에 유용합니다.
- 왜 중요한가?
- 분자의 안정성이나 반응성 등을 예측하려면 기저 상태 에너지 계산이 필요
- 전통적인 컴퓨터로는 매우 복잡한 분자 시스템의 에너지를 정확히 계산하기 어려움
- VQE는 양자 상태로부터 기저 에너지를 효과적으로 추정 가능
- Qiskit에서 VQE 구현 가능
- 다양한 Ansatz, 옵티마이저, 시뮬레이터 선택 가능
3. QAOA: Quantum Approximate Optimization Algorithm
그래프 이론 등의 조합 최적화 문제를 해결하기 위한 양자 알고리즘. MaxCut 문제가 대표 예시입니다.
- MaxCut 문제란?
- 그래프의 노드들을 두 그룹으로 나눠서, 연결된 간선이 최대한 많이 두 그룹 사이에 놓이도록 분할
- 현실 세계에서는 네트워크 설계, 일정 배정, 전력망 구성 등 다양한 분야에 적용
- QAOA 특징
- 양자 회로로 문제를 모델링하고, 최적화된 해를 근사적으로 구함
- 향후 양자 우위(quantum advantage) 실현 가능성이 높은 분야 중 하나
- **AQC (Adiabatic Quantum Computing)**과 연계
- QAOA는 AQC에서 아이디어를 차용했으며, 디지털 방식으로 구현
4. Variational Quantum Machine Learning
입문 설명: 양자 회로를 머신러닝 모델처럼 파라미터화하고, 고전적인 방법으로 학습을 수행
- 예: 양자 신경망, 양자 분류기 등
- 양자 회로가 데이터를 임베딩하고, 고전 알고리즘이 파라미터를 업데이트
5. Qiskit 실습
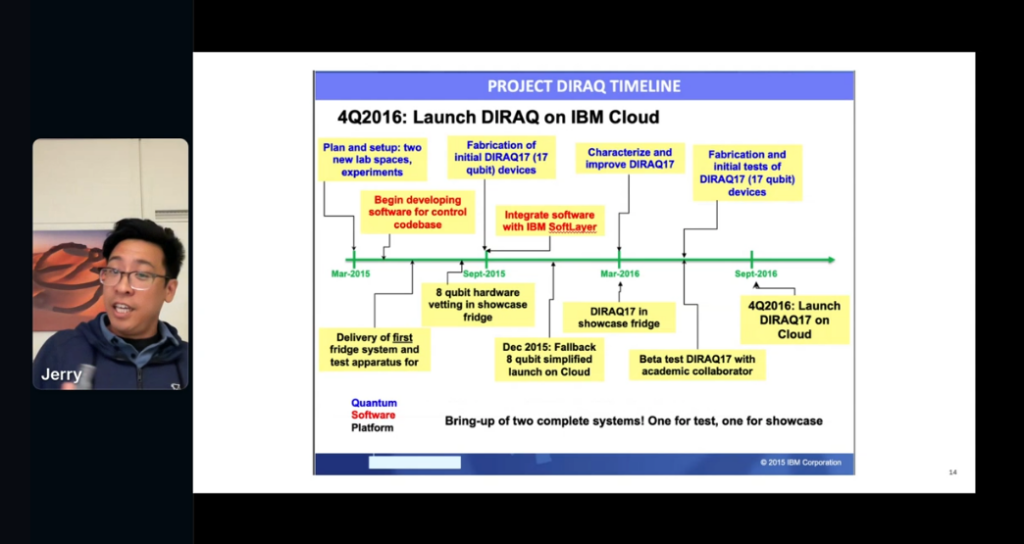
S4: Quantum Computers on the Cloud by Jerry Chow